小帅的博客

LeetCode Hot 100 (6) 矩阵

1/7/2024 LeetCode

# 73. 矩阵置零 (opens new window)

给定一个 m x n 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用 原地 (opens new window) 算法。

示例 1：

img

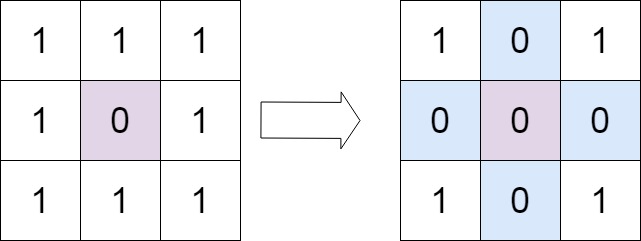
输入：matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出：[[1,0,1],[0,0,0],[1,0,1]]
1
2

示例 2：

img

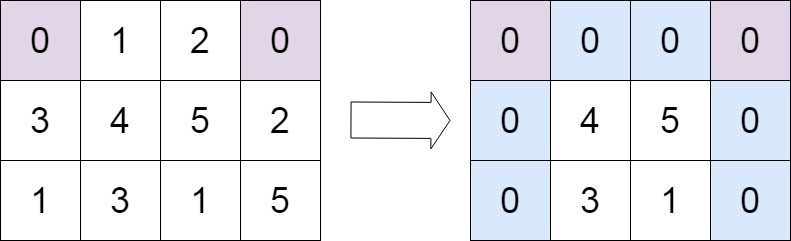
输入：matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出：[[0,0,0,0],[0,4,5,0],[0,3,1,0]]
1
2

提示：

  • m == matrix.length
  • n == matrix[0].length
  • 1 <= m, n <= 200
  • -2^31 <= matrix[i][j] <= 2^31 - 1

进阶：

  • 一个直观的解决方案是使用 O(mn) 的额外空间，但这并不是一个好的解决方案。
  • 一个简单的改进方案是使用 O(m + n) 的额外空间，但这仍然不是最好的解决方案。
  • 你能想出一个仅使用常量空间的解决方案吗？

思路：

用第一行和第一列的数是否为0来判断某行某列是否为0，用两个标志表示第一行和第一列是否需要全变为0。

代码：

C++代码

class Solution {
public:
    void setZeroes(vector<vector<int>>& matrix) {
        bool flagRow = false;
        int m = matrix.size();
        int n = matrix[0].size();
        for(int i=0;i<n;i++) {
            if(matrix[0][i]==0) {
                flagRow = true;
            }
        }
        bool flagCol = false;
        for(int i=0;i<m;i++) {
            if(matrix[i][0]==0) {
                flagCol = true;
            }
        }
        for(int i=1;i<m;i++) {
            for(int j=1;j<n;j++) {
                if(matrix[i][j]==0) {
                    matrix[i][0] = 0;
                    matrix[0][j] = 0;
                }
            }
        }
        for(int i=1;i<m;i++) {
            if(matrix[i][0]==0) {
                for(int j=1;j<n;j++) {
                    matrix[i][j] = 0;
                }
            }
        }
        for(int i=1;i<n;i++) {
            if(matrix[0][i]==0) {
                for(int j=1;j<m;j++) {
                    matrix[j][i] = 0;
                }
            }
        }
        if(flagRow) {
            for(int i=0;i<n;i++) {
                matrix[0][i] = 0;
            }
        }
        if(flagCol) {
            for(int i=0;i<m;i++) {
                matrix[i][0] = 0;
            }
        }
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

Go代码

func setZeroes(matrix [][]int)  {
    m := len(matrix) 
    n := len(matrix[0])
    flagRow := false
    for i:=0;i<n;i++ {
        if matrix[0][i] == 0 {
            flagRow = true
        } 
    }
    flagCol := false
    for i:=0;i<m;i++ {
        if matrix[i][0] == 0 {
            flagCol = true
        }
    }
    for i:=1;i<m;i++ {
        for j:=1;j<n;j++ {
            if matrix[i][j] == 0 {
                matrix[i][0] = 0
                matrix[0][j] = 0
            }
        }
    }
    for i:=1;i<m;i++ {
        if matrix[i][0] == 0 {
            for j:=1;j<n;j++ {
                matrix[i][j] = 0
            }
        }
    }
    for i:=1;i<n;i++ {
        if matrix[0][i] == 0 {
            for j:=1;j<m;j++ {
                matrix[j][i] = 0
            }
        }
    }
    if flagRow {
        for i:=0;i<n;i++ {
            matrix[0][i] = 0
        }
    }
    if flagCol {
        for i:=0;i<m;i++ {
            matrix[i][0] = 0
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

# 54. 螺旋矩阵 (opens new window)

题目：

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

示例 1：

img

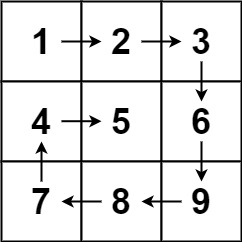
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]
1
2

示例 2：

img

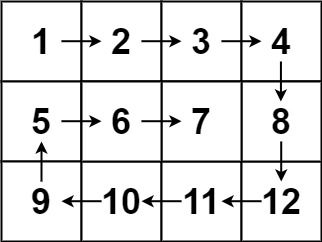
输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出：[1,2,3,4,8,12,11,10,9,5,6,7]
1
2

提示：

  • m == matrix.length
  • n == matrix[i].length
  • 1 <= m, n <= 10
  • -100 <= matrix[i][j] <= 100

思路：

模拟 用一个二维数组表示四种变化，当下一个坐标越界或者遍历过时需要转到下一种变化

代码：

C++代码

class Solution {
public:
    vector<int> spiralOrder(vector<vector<int>>& matrix) {
        int x = 0, y = 0;
        vector<vector<int>> di = {{0,1},{1,0},{0,-1},{-1,0}};
        int m = matrix.size();
        int n = matrix[0].size();
        vector<vector<int>> flag(m,vector<int>(n,-1));
        int k = m*n;
        int t = 0;
        vector<int> res;
        while(k--) {
            res.push_back(matrix[x][y]);
            flag[x][y] = 0;
            int dx = x + di[t][0];
            int dy = y + di[t][1];
            if(dx<0||dx>=m||dy<0||dy>=n||flag[dx][dy]==0) {
                t = (t+1)%4;
            }
            x = x + di[t][0];
            y = y + di[t][1];
        }
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

Go代码

func spiralOrder(matrix [][]int) []int {
    m := len(matrix)
    n := len(matrix[0])
    di := [][]int{{0,1},{1,0},{0,-1},{-1,0}}
    flag := make([][]int,m)
    for i:=0;i<m;i++ {
        flag[i] = make([]int,n)
    }
    x := 0
    y := 0
    t := 0
    k := m*n
    res := make([]int,0) 
    for k!=0 {
        k--
        res = append(res,matrix[x][y])
        flag[x][y] = 1
        dx := x + di[t][0]
        dy := y + di[t][1]
        if dx<0||dx>=m||dy<0||dy>=n||flag[dx][dy]==1 {
            t = (t+1)%4
        }
        x = x + di[t][0]
        y = y + di[t][1]
    }
    return res
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

# 48. 旋转图像 (opens new window)

题目：

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在原地 (opens new window) 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

示例 1:

img

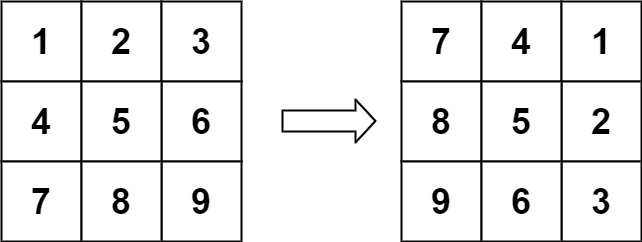
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]
1
2

示例 2:

img

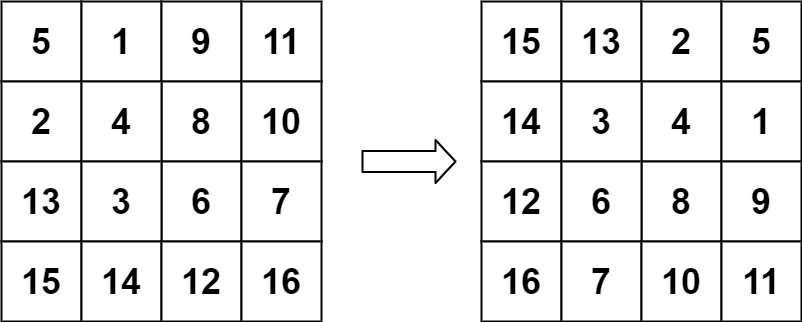
输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]
1
2

提示：

  • n == matrix.length == matrix[i].length
  • 1 <= n <= 20
  • -1000 <= matrix[i][j] <= 1000

思路：

先将上下的横排反转，然后按照左上右下的轴进行反转

代码：

C++代码

class Solution {
public:
    void rotate(vector<vector<int>>& matrix) {
        int m = matrix.size();
        int n = matrix[0].size();
        for(int i=0;i<m/2;i++) {
            for(int j=0;j<n;j++) {
                swap(matrix[i][j],matrix[n-1-i][j]);
            }
        }
        for(int i=1;i<m;i++) {
            for(int j=0;j<i;j++) {
                swap(matrix[i][j],matrix[j][i]);
            }
        }
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

Go代码

func rotate(matrix [][]int)  {
    m := len(matrix)
    n := len(matrix[0])
    for i:=0;i<m/2;i++ {
        for j:=0;j<n;j++ {
            matrix[i][j], matrix[n-1-i][j] = matrix[n-1-i][j], matrix[i][j]
        }
    }
    for i:=1;i<m;i++ {
        for j:=0;j<i;j++ {
            matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

# 240. 搜索二维矩阵 II (opens new window)

题目：

编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

  • 每行的元素从左到右升序排列。
  • 每列的元素从上到下升序排列。

示例 1:

img

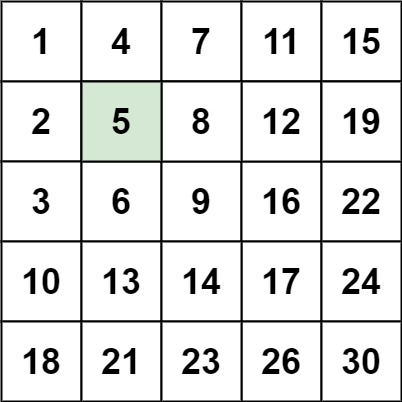
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出：true
1
2

示例 2:

img

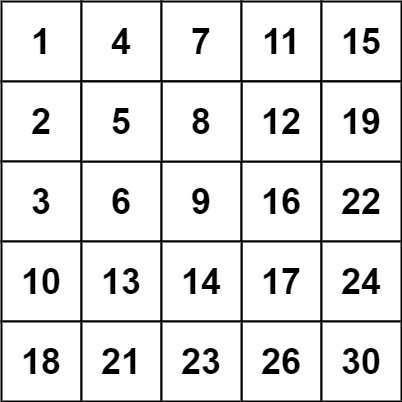
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
输出：false
1
2

提示：

  • m == matrix.length
  • n == matrix[i].length
  • 1 <= n, m <= 300
  • -10^9 <= matrix[i][j] <= 10^9
  • 每行的所有元素从左到右升序排列
  • 每列的所有元素从上到下升序排列
  • -10^9 <= target <= 10^9

思路：

从右上角开始搜索，如果当前值比目标值大则往左侧搜索（因为当前列下面的更大），否则忘下侧搜索（当前行左侧更小）

代码：

C++代码

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int m = matrix.size();
        int n = matrix[0].size();
        int x = 0, y = n-1;
        while(true) {
            if (x>=m||y<0) {
                return false;
            } 
            if(matrix[x][y]==target) {
                return true;
            } else if(matrix[x][y]>target) {
                y--;
            } else {
                x++;
            }
        }
        return false;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

Go代码

func searchMatrix(matrix [][]int, target int) bool {
    m := len(matrix)
    n := len(matrix[0])
    x := 0
    y := n-1
    for true {
        if x==m||y==-1 {
            return false
        }
        if matrix[x][y]==target {
            return true
        } else if matrix[x][y]>target {
            y--
        } else {
            x++
        }
    }
    return false
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19